Simple logistic regression with RIM

RIM (regularised mutual information) is a proposal of model by Krause et al. (2010) which consists in maximising for a linear model under \(\ell_2\) penalty. In this example, we show how to do clustering of a Gaussian mixture using RIM.

import numpy as np
from matplotlib import pyplot as plt
from sklearn import datasets

from gemclus.linear import RIM

Load a simple synthetic dataset

# Generate samples on that are simple to separate
X, y = datasets.make_blobs(centers=3, cluster_std=0.5, n_samples=200, random_state=0)

Train the model

Create the RIM clustering model (just a logistic regression) and fit it to the data.

clf = RIM(n_clusters=3, reg=1e-1, random_state=0)
clf.fit(X)

RIM(random_state=0)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

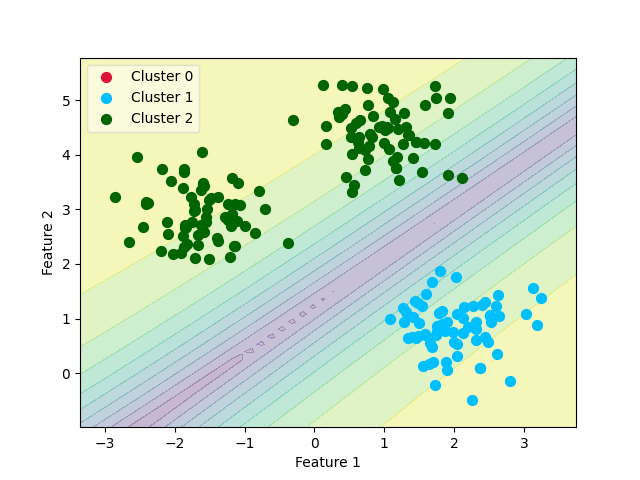
Final Clustering

Let us take a look at the decision boundaries according to the probabilities

# Predict a grad of inputs
x_vals = np.linspace(X[:, 0].min() - 0.5, X[:, 0].max() + 0.5, num=50)
y_vals = np.linspace(X[:, 1].min() - 0.5, X[:, 1].max() + 0.5, num=50)
xx, yy = np.meshgrid(x_vals, y_vals)
grid_inputs = np.c_[xx.ravel(), yy.ravel()]
grid_pred = clf.predict_proba(grid_inputs)

# Isolate probability of the argmax
zz = grid_pred.max(1)
zz = zz.reshape((50, 50))

plt.contourf(xx, yy, zz, alpha=0.3, levels=10)

# Now, show the cluster predictions
y_pred = clf.predict(X)
X_0 = X[y_pred == 0]
X_1 = X[y_pred == 1]
X_2 = X[y_pred == 2]

ax0 = plt.scatter(X_0[:, 0], X_0[:, 1], c='crimson', s=50)
ax1 = plt.scatter(X_1[:, 0], X_1[:, 1], c='deepskyblue', s=50)
ax2 = plt.scatter(X_2[:, 0], X_2[:, 1], c='darkgreen', s=50)

leg = plt.legend([ax0, ax1, ax2],
                 ['Cluster 0', 'Cluster 1', 'Cluster 2'],
                 loc='upper left', fancybox=True, scatterpoints=1)
leg.get_frame().set_alpha(0.5)

plt.xlabel('Feature 1')
plt.ylabel('Feature 2')

plt.show()

print(clf.score(X))

0.44865384782317197