Graph node clustering with a nonparametric model

We create here a random graph by following a simplified version of the Latent Position Model generative procedure. To create the graph, we sample latent positions from a Gaussian Mixture Model and create a graph with as many nodes as samples. Edges are then determined according to probability depending only on the distance between samples.

To perform clustering, we then use a nonparametric model which will associated to each node a clustering probability. We indicate to this model a specific distance that is adequate for our graph nodes. Note that the parameters given to the fit function instead of the data is a simple identity matrix.

import itertools

import numpy as np
from matplotlib import pyplot as plt
from scipy.sparse import csgraph
from sklearn import metrics

from gemclus import data
from gemclus.nonparametric import CategoricalWasserstein

Draw samples from a GMM

# Generate samples on that are simple to separate
N = 100  # Number of nodes in the graph
# GMM parameters
means = np.array([[1, -1], [1, 1], [-1, -1], [-1, 1]])*3
covariances = [np.eye(2)]*4
X, y = data.draw_gmm(N, means, covariances, np.ones(4) / 4, random_state=0)

Create the graph edges

distances = metrics.pairwise_distances(X, metric="euclidean")
edge_probs = np.exp(-distances)

np.random.seed(0)
adjacency_matrix = np.random.binomial(n=1, p=edge_probs)  # Determine if there is an edge from node i->j

# Make the adjacency matrix symmetric
adjacency_matrix = np.maximum(adjacency_matrix, adjacency_matrix.T)

Pre-compute a specific metric between samples

# compute the all-pairs shortest path in this graph
distances = csgraph.floyd_warshall(adjacency_matrix, directed=False, unweighted=True)

# Replace np.inf with 2 times the size of the matrix
distances[np.isinf(distances)] = 2 * distances.shape[0]

Train the model

Create the Non parametric GEMINI clustering model and call the .fit method to optimise the cluster assignment of the nodes

# We specify a custom metric and will pass the distance matrix to the `y` argument of `.fit`.
model = CategoricalWasserstein(n_clusters=4, metric="precomputed", ovo=True, random_state=1789, learning_rate=1e-1)
# In the nonparametric model, X is a dummy unnecessary variable because the parameters do not depend on the values
# of X. There is only an index matching.
y_pred = model.fit_predict(np.eye(N), y=distances)

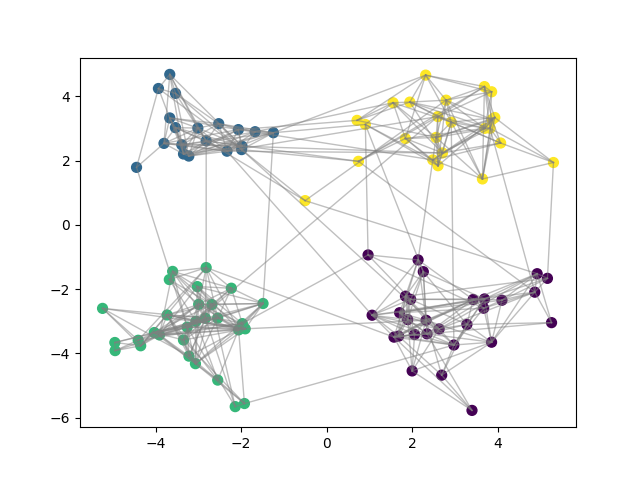
Final Clustering

for node_i, node_j in itertools.combinations(range(N),2):
    if adjacency_matrix[node_i,node_j]:
        plt.plot([X[node_i,0],X[node_j,0]], [X[node_i,1],X[node_j,1]], c="gray",linewidth=1,alpha=0.5)
plt.scatter(X[:, 0], X[:, 1], c=y_pred, s=50)
plt.show()

ari_score = metrics.adjusted_rand_score(y, y_pred)
gemini_score = model.score(np.eye(N), y=distances)
print(f"Final ARI score: {ari_score:.3f}")
print(f"GEMINI score is {gemini_score:.3f}")

Final ARI score: 0.977
GEMINI score is 2.141