Note
Go to the end to download the full example code.
Extending GemClus to build your own discriminative clustering model¶
It is possible that the model we wish to use is not available among the choices of GemClus. To that end, it is possible to extend the framework and define custom models that can still be trained by GEMINI.
In this example, we define a simple bias-less logistic regression for 2 classes with a sigmoid activation function and train it to tell apart two isotropic Gaussian distributions.
The model can be written as:
\[p_\theta(y=1|x) = \text{sigmoid}(x^\top \theta)\]
import numpy as np
import matplotlib.pyplot as plt
from gemclus import DiscriminativeModel
from gemclus.data import draw_gmm
Create the custom model¶
class BinaryRegression(DiscriminativeModel):
# We start by defining the same parameters as expected by the parent class for Discriminative model
def __init__(self, n_clusters=3, gemini="mi", max_iter=1000, learning_rate=1e-3, solver="adam", batch_size=None,
verbose=False, random_state=None):
super().__init__(
n_clusters=n_clusters,
gemini=gemini,
max_iter=max_iter,
learning_rate=learning_rate,
solver=solver,
batch_size=batch_size,
verbose=verbose,
random_state=random_state
)
def _init_params(self, random_state, X=None):
# We define the initialisation of our parameters using the random state
in_threshold = np.sqrt(1 / X.shape[1])
self.theta_ = random_state.uniform(-in_threshold, in_threshold, size=(X.shape[1], 1))
def _get_weights(self):
# For the optimiser, all parameters that can be optimised need to be returned inside a list
return [self.theta_]
def _infer(self, X, retain=True):
# This function computes the output of the model. You must ensure to have a probability vector
y_pred_logit = np.matmul(X, self.theta_)
# Compute sigmoid of prediction
y_pred = 1 / (1.0 + np.exp(-y_pred_logit))
if retain:
# The retain flag here means that we are allowed to store intermediate information
# For example, information useful for backpropagation
self._y_sigmoid = y_pred
# As the GEMINI objectives expect arrays to be of shape (n_samples, n_clusters), we duplicate
# the opposite probability on the column axis
y_pred = np.concatenate([y_pred.reshape((-1, 1)), (1 - y_pred).reshape((-1, 1))], axis=1)
# It is important that the columns add up to 1 for each row, otherwise the GEMINI will not work
return y_pred
def _compute_grads(self, X, y_pred, gradient):
# The gradient has a shape of (n_samples, n_clusters) following the prediction we used in `_infer`
# We first start our gradient by correcting the column axis extension
gradient = gradient[:, 0] - gradient[:, 1]
# We apply the gradient of the sigmoid
gradient = self._y_sigmoid * (1 - self._y_sigmoid) * gradient.reshape((-1, 1))
# And we finish with the gradient on our model parameter
theta_grad = np.matmul(X.T, gradient)
# We return this gradient inside a list. The order of gradients must be matching the order of the parameters
# in `_get_weights`
# As the goal of GEMINI is to maximise contrary to common framework which aim for minimisation,
# we return the negative of the gradient
return [-theta_grad]
Test the fitting procedure and plot the clustering results¶
# We can test this model
X, y = draw_gmm(n=100, loc=np.eye(2), scale=[np.eye(2) * 0.2, np.eye(2) * 0.2], pvals=np.ones(2) / 2, random_state=0)
custom_model = BinaryRegression(gemini="wasserstein_ovo", n_clusters=2)
y_pred = custom_model.fit_predict(X)
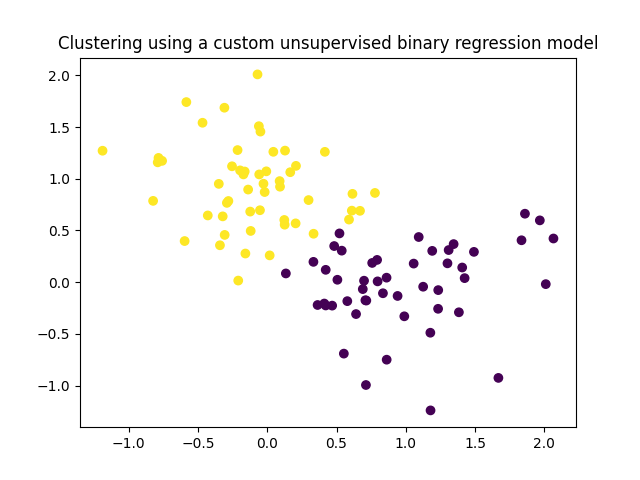
plt.title("Clustering using a custom unsupervised binary regression model")
plt.scatter(X[:, 0], X[:, 1], c=y_pred)
plt.show()
Total running time of the script: (0 minutes 1.725 seconds)