Clustering circles with kernel RIM

We show here a simple dataset consisting in two centred circle that can be challenging for some clustering algorithms. We solve this case using the kernel RIM algorithm. This algorithm fits a logistic regression on the kernel matrix derived from the dataset.

from matplotlib import pyplot as plt
from sklearn import datasets
from sklearn import metrics

from gemclus.linear import KernelRIM

Draw samples for the circle dataset

# We start by generating samples distributed on two circles
noise = 0.05
factor = 0.1
X, y = datasets.make_circles(n_samples=200, noise=noise, factor=factor, random_state=0)

Training clustering model

model_kernel = KernelRIM(n_clusters=2, base_kernel="laplacian", max_iter=1000, reg=4/len(X), random_state=0)
y_pred = model_kernel.fit_predict(X)
print(f"ARI = {metrics.adjusted_rand_score(y, y_pred)}")

ARI = 1.0

Show predictions on similar samples

# Create a novel set of samples and cluster them
new_X, new_y = datasets.make_circles(n_samples=200, noise=noise, factor=factor, random_state=1)
new_pred = model_kernel.predict(new_X)
print(f"ARI = {metrics.adjusted_rand_score(new_y, new_pred)}")


plt.scatter(X[:, 0], X[:, 1], c=y_pred, marker="+", label="Training samples")
plt.scatter(new_X[:, 0], new_X[:, 1], c=new_pred, marker="o", label="Testing samples")
plt.legend()
plt.show()

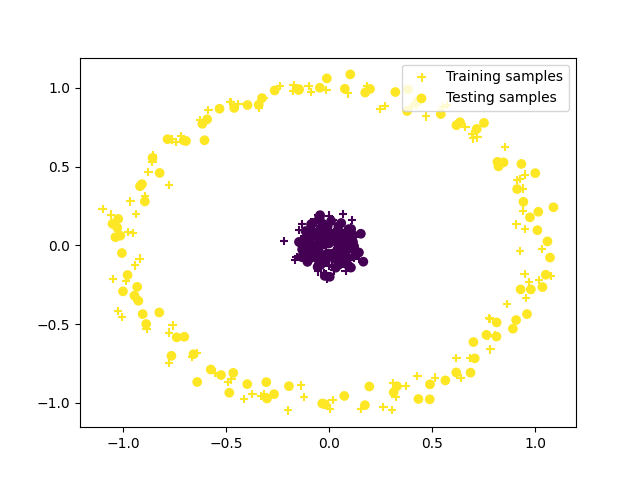
ARI = 1.0