Note
Go to the end to download the full example code.
Consensus clustering with linking constraints on sample pairs¶
We show in this example how to:
Perform consensus clustering using gemclus
Improve the results by enforcing constraints on the clustering models
Consensus clustering is loosely an equivalent to ensemble methods in unsupervised learning where we seek to find a clustering in agreeance with multiple clustering methods. A matrix describing the ratio of times samples were clustered together is used as a metric to provide guidance for a final clustering model.
Then, to ensure that some samples remain together or apart, we add must-link / cannot-link constraints on the clustering model. While not all constraints may be satisfied, the proposed solution will try its best to be in agreeance with the low-level clustering results and the supervised inputs.
The advantage of such constraints is that they do not require knowledge on the true class of the data, but rather a simple idea of whether samples can go together or not.
# We start by loading
from gemclus.nonparametric import CategoricalWasserstein
from gemclus.linear import LinearMMD
from gemclus.data import celeux_one
from gemclus import add_mlcl_constraint
import itertools
import numpy as np
from sklearn import metrics
import matplotlib.pyplot as plt
Load the dataset¶
# We take a small challenging dataset with 3 clusters where the true cluster means are close
X,y = celeux_one(n=100, p=5, mu=0.6, random_state = 0)
Multiple model clustering¶
# We fit several model on this dataset with various kernel
np.random.seed(0)
all_models = [LinearMMD(n_clusters=3, kernel=x, learning_rate=1e-2, ovo=True) for x in ["linear", "cosine", "sigmoid", "rbf"]]
for i in range(len(all_models)):
all_models[i].fit(X)
# How do our models perform on this dataset?
for model in all_models:
print("Sub-model ARI: ", metrics.adjusted_rand_score(model.predict(X), y))
Sub-model ARI: 0.11914066061963555
Sub-model ARI: 0.11176053892324672
Sub-model ARI: 0.11421905413971052
Sub-model ARI: 0.22472124150185058
Build the consensus matrix¶
# Build the consensus matrix, i.e. the number of times pairs of samples
# were in the same cluster
consensus_matrix = np.zeros(shape=(len(X), len(X)))
for i in range(len(all_models)):
y_pred = all_models[i].predict(X)
for i,j in itertools.combinations_with_replacement(range(len(X)), r=2):
consensus_matrix[i,j] += int(y_pred[i]==y_pred[j])
consensus_matrix[j,i] = consensus_matrix[i,j]
consensus_matrix /= len(all_models)
Create the consensus clustering model¶
We will use a nonparametric model and provide 1-consensus_matrix as the precomputed metric for the model. Notice that the parameter X is here for API consistency, although superfluous
consensus_model = CategoricalWasserstein(n_clusters=3, random_state = 0, metric="precomputed")
consensus_model.fit(X, 1-consensus_matrix)
y_pred_consensus = consensus_model.predict_proba(X)
# What are our consensus performances?
print("Consensus ARI: ", metrics.adjusted_rand_score(y_pred_consensus.argmax(1), y))
Consensus ARI: 0.10728640074310927
Optimise the results with linking constraints¶
We will enforce some pairs of samples to be together or apart. While in this simulation we use the class y to extrapolate this pairs, real life situation would emphasize more on a field expert to provide such knowledge.
We will try to use the samples that have the most confident predictions
sorted_confidence_samples = sorted(range(len(X)), key=lambda i: y_pred_consensus[i].max(), reverse=True)
must_link = []
unsure_sample_pairs = itertools.combinations(sorted_confidence_samples, 2)
while len(must_link)!=10:
i,j = next(unsure_sample_pairs)
if y[i]==y[j] and y_pred_consensus[i].argmax()!=y_pred_consensus[j].argmax():
if (i,j) not in must_link:
must_link += [(i,j)] # Sample i and j must be together
cannot_link = []
unsure_sample_pairs = itertools.combinations(sorted_confidence_samples, 2)
while len(cannot_link)!=10:
i,j = next(unsure_sample_pairs)
if y[i]!=y[j] and y_pred_consensus[i].argmax()==y_pred_consensus[j].argmax():
if (i,j) not in must_link:
cannot_link += [(i,j)] # Sample i and j should not be together
Add must-link / cannot-link constraint¶
We start over with the same model for consensus
base_model = CategoricalWasserstein(n_clusters=3, random_state=0, metric="precomputed")
# This line decorates the base model to enforce must-link / cannot-link constraints
mlcl_consensus_model = add_mlcl_constraint(base_model, must_link, cannot_link)
mlcl_consensus_model.fit(X, 1-consensus_matrix)
y_pred_mlcl_consensus = mlcl_consensus_model.predict(X)
print("ARI of constrained consensus: ", metrics.adjusted_rand_score(y, y_pred_mlcl_consensus))
ARI of constrained consensus: 0.16976700304809886
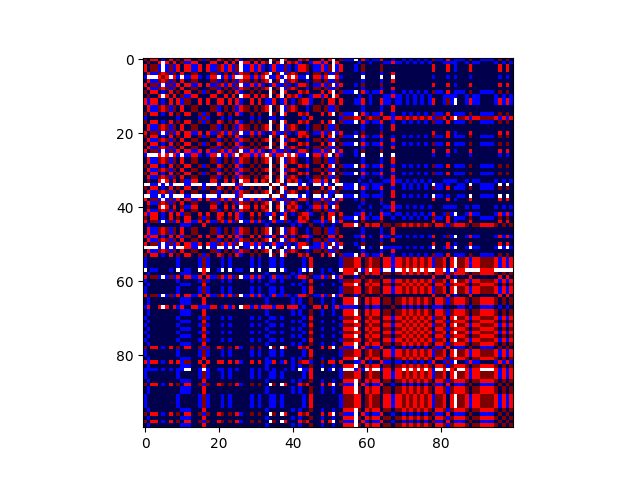
Plotting the consensus matrix¶
consensus_order = np.argsort(y_pred_mlcl_consensus)
plt.imshow(consensus_matrix[consensus_order][:,consensus_order], cmap="seismic")
plt.show()
Total running time of the script: (0 minutes 8.575 seconds)