gemclus.gemini.ChiSquareGEMINI

class gemclus.gemini.ChiSquareGEMINI(ovo=False, epsilon=1e-12)

Implements the one-vs-all and one-vs-one Chi Squared divergence GEMINI.

The one-vs-all version compares the chi square divergence between a cluster distribution and the data distribution.

\[\mathcal{I} = \mathbb{E}_{y \sim p(y)}[D_{\chi^2}(p(x|y)\|p(x))]\]

The one-vs-one version compares the chi square divergence between two cluster distributions.

\[\mathcal{I} = \mathbb{E}_{y_a,y_b \sim p(y)}[D_{\chi^2}(p(x|y_a)\|p(x|y_b))]\]

Parameters:

ovo: bool, default=False

Whether to use the one-vs-all objective (False) or the one-vs-one objective (True).

epsilon: float, default=1e-12

The precision for clipping the prediction values in order to avoid numerical instabilities.

References

Sugiyama, M., Yamada, M., Kimura, M., & Hachiya, H. (2011). On information-maximization clustering: Tuning parameter selection and analytic solution. In Proceedings of the 28th International Conference on Machine Learning (ICML-11) (pp. 65-72).

__init__(ovo=False, epsilon=1e-12)

compute_affinity(X, y=None)

Unused for f-divergences.

Returns:

None

evaluate(y_pred, affinity, return_grad=False)

Compute the GEMINI objective given the predictions \(p(y|x)\) and an affinity matrix. The computation must return as well the gradients of the GEMINI w.r.t. the predictions. Depending on the context, the affinity matrix affinity can be either a kernel matrix or a distance matrix resulting from the compute_affinity method.

Parameters:

y_pred: ndarray of shape (n_samples, n_clusters)

The conditional distribution (prediction) of clustering assignment per sample.

affinity: ndarray of shape (n_samples, n_samples)

The affinity matrix resulting from the compute_affinity method. The matrix must be symmetric.

return_grad: bool, default=False

If True, the method should return the gradient of the GEMINI w.r.t. the predictions \(p(y|x)\).

Returns:

gemini: float

The gemini score of the model given the predictions and affinities.

gradients: ndarray of shape (n_samples, n_clusters)

The derivative w.r.t. the predictions y_pred: \(\nabla_{p (y|x)} \mathcal{I}\)

Examples using gemclus.gemini.ChiSquareGEMINI

Clustering with the squared-loss mutual information

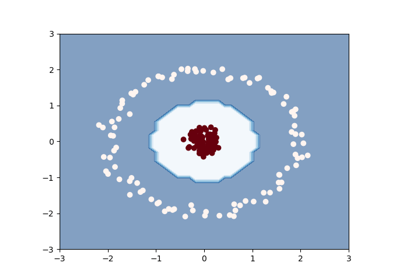
Clustering with the squared-loss mutual information